12 заданий на ЕГЭ по профильной математике, которые лучше решить в первую очередь
ЕГЭ по математике профильного уровня — довольно сложный экзамен.
Этот экзамен сдают все, кому математика нужна для поступления в университет, например будущие программисты и физики. Цель здесь — набрать как можно больше баллов. Практика показывает, что некоторые задачи ребята решают успешнее других. Расскажем о них и разберем примеры.
Мы включили задания из разных частей экзамена, в том числе посложнее и даже самое сложное. Баллы за них можно заработать, даже если решить только часть или ошибиться в расчетах. К этим заданиям можно подходить не сразу, а например, когда в чем-то не уверены в первой части, но готовы приступить ко второй.
Какие задания профильного уровня разберем
Как проходит экзамен
Профильный экзамен делится на две части — всего 19 заданий. Решить их нужно за 3 часа 55 минут.
В первой части 12 заданий — здесь записывают в бланк только краткий ответ:
- семь заданий базового уровня сложности — № 1—4, 6—8;
- пять заданий повышенного уровня сложности: № 5, 9—12.
За каждое задание первой части можно получить 1 первичный балл. Если верно решить все задания отсюда, заработаете 12 первичных баллов по шкале перевода 2025. Если перевести их в тестовый балл, получится 70, а это неплохой результат. Например, в 2024 году математику профильного уровня сдавали около 290 тысяч участников, средний балл — 62,55.
Во второй части пять заданий повышенного уровня — с 13 по 17. Дальше следуют два задания высокого уровня сложности — 18 и 19: в них решения записывают целиком, их проверяет эксперт.
Если решить все 12 заданий из этого материала, вы наберете 18 первичных баллов — это 82 тестовых.
На базовой математике вместе с заданиями дают справочный материал со множеством формул и пояснений. А справочный материал на профильной математике содержит только четыре формулы — остальные нужно или знать наизусть, или уметь выводить их.
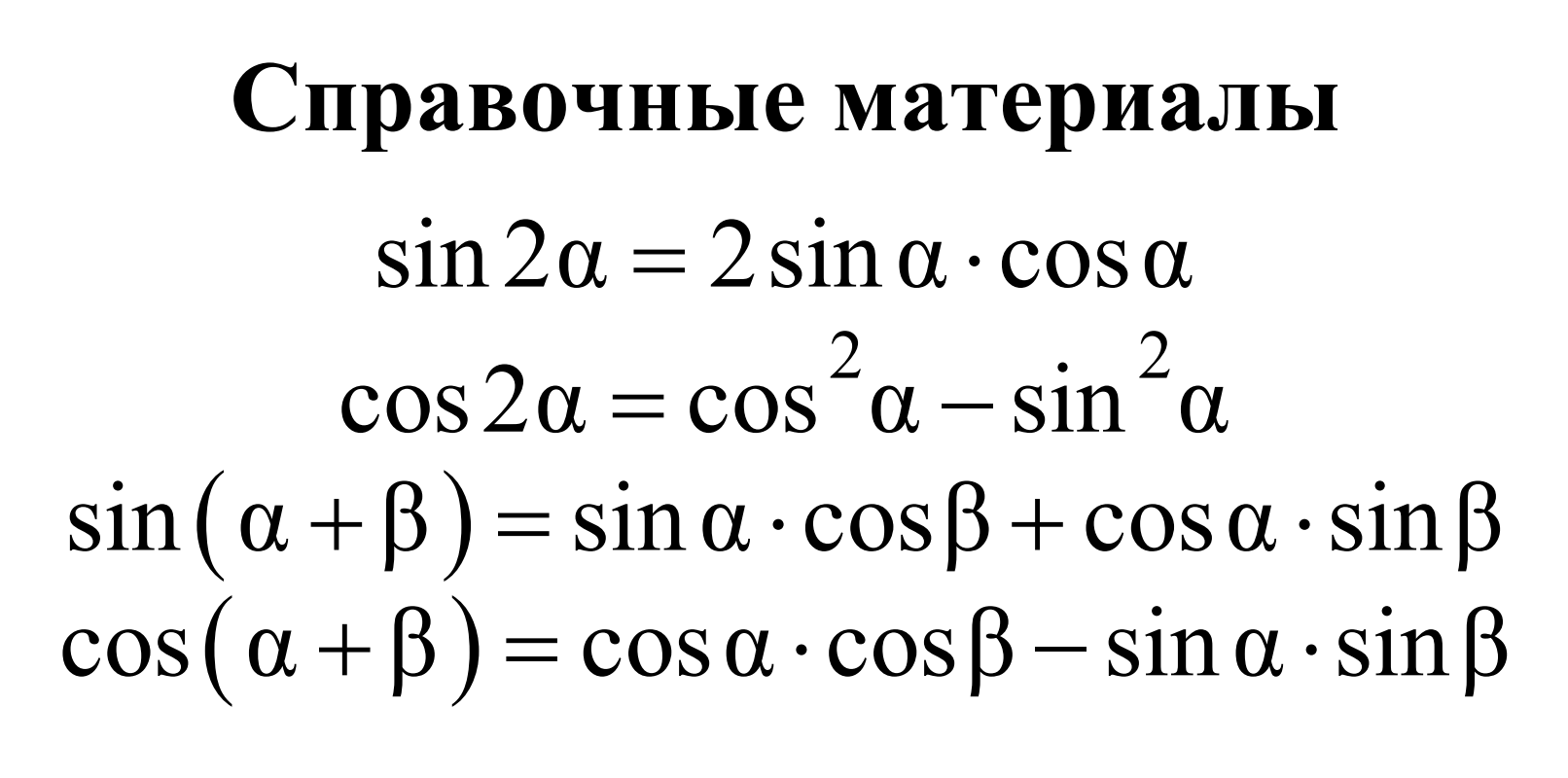
Первое задание
Задача на работу с геометрическими фигурами: треугольником, ромбом, параллелограммом и так далее.
Что знать. Формулы из курса геометрии за 7—9 классы.
Совет. Систематизируйте материал по фигурам. На листе изобразите, например, треугольник, запишите его свойства, формулы для площади и так далее. Лучше набросать самому, но можно взять и готовые материалы в интернете.

Второе задание
Проверяет умение оперировать векторами, их координатами, суммой, произведением и так далее.
Что знать. Прежде всего запомните:
- понятия равных и коллинеарных векторов;
- как найти координаты вектора по заданным координатам его начала и конца и когда вектор расположен в прямоугольной системе координат или на линованной бумаге;
- как найти координаты вектора по координатам его начала и конца;
- как найти длину вектора по координатам вектора и по координатам начала и конца;
- формулы скалярного произведения векторов по координатам самого вектора, а также по длинам векторов и углу между ними;
- формулы сложения и вычитания векторов, умножения вектора на число;
- как выполнять действия с векторами, используя правило треугольника и параллелограмма.
Совет. Потренируйтесь находить координаты вектора в системе координат алгебраическим или геометрическим способами. Помните, что длина вектора всегда положительна, скалярное произведение перпендикулярных векторов равно 0, а координаты коллинеарных векторов пропорциональны.

Третье задание
Задачи по стереометрии: на нахождение объема, площади.
Что знать. Прежде всего — формулы и свойства объемов и площадей поверхностей параллелепипеда, шара, куба, цилиндра и конуса. Еще нужно иметь представление о сечениях многогранников и фигур вращения и уметь строить сечения самостоятельно.
Совет. Нелишне отработать алгоритм построения сечений и повторить формулы для площадей плоских фигур — например, чтобы найти площадь сечения.
Иногда здесь встречаются простые задания: например, в цилиндр вписан конус того же основания и нужно найти объем одной из фигур. Если знаете формулы, быстро вычислите: объем вписанного в цилиндр конуса всегда в три раза меньше, чем объем самого цилиндра. Соответственно, объем цилиндра в три раза больше. А объем шара, вписанного в цилиндр, всегда занимает две трети объема.

Шестое задание
Проверяет умение решать базовые уравнения.
Что знать. Повторите свойства степеней, условия существования корня четной степени, логарифмов и дробей с неизвестным знаменателем. Также пробегитесь по алгоритмам решения простейших тригонометрических, показательных, логарифмических и иррациональных уравнений. Последние два требуют проверить найденное значение неизвестной переменной или определить область допустимых значений.
Совет. В любом уравнении можно выполнить проверку. Это займет секунды, но даст понять, верно ли решили задачу. При проверке левую и правую части уравнения решайте отдельно и только потом сравнивайте полученные значения и делайте выводы. Еще рекомендую прописывать вычисления в черновике — это уменьшит риск ошибок при подсчете.

Седьмое задание
Здесь проверяют умение вычислять значения выражений и выполнять их преобразования.
Что знать. Повторите формулы для степеней, корней n-степени, логарифмов, тригонометрические формулы и знаки тригонометрических функций по четвертям.
Отдельно повторите дроби:
- правила сокращения алгебраических дробей: прежде чем сократить, разложите на множители числитель и знаменатель.
- свойства дробей.
Также помните, что свойства степеней и логарифмов работают как в прямом, так и в обратном порядке.
Совет. Помните, что все формулы можно применять как слева направо, так и справа налево.
Если не знаете, с чего начать решение, подумайте:
- По какой теме задача.
- Что помните по теме.
- Если ранее решали задания по теме, что мешает решить его сейчас.

Восьмое задание
Задание на оперирование функциями. Оно представлено или в виде текста — в основном на физический смысл производной, или в виде графика.
Что знать. Вот что следует повторить:
- Основные свойства функций. Возрастание и убывание, наибольшее и наименьшее значение.
- Геометрический и физический смысл производной.
- Правила нахождения производных.
- Связь между монотонностью функции и знаком ее производной.
- Связь между графиком производной и свойствами самой функции.
Совет. Полезно сочетать работу по графику самой функции и графику производной функции. На них по-разному вычисляют:
- точки максимума и минимума функции;
- промежутки возрастания и убывания функции;
- значение производной в точке;
- наибольшее и наименьшее значения функции.
Научитесь строить график производной функции по заданному графику самой функции и наоборот. Это умение показывает глубину владения производными.

Девятое задание
Моделирование реальных ситуаций на языке математики и составление выражений, уравнений, неравенств по условию задачи.
Что знать. Вот что пригодится:
- Алгоритмы решения уравнений всех видов.
- Умение выражать из формулы одну величину через известные другие.
- Уметь работать с многозначными числами вида а × 10n, с десятичными и обыкновенными дробями.
Совет. При подготовке обратите внимание на задачи, где важно понять физический смысл условия — когда после подстановки известных величин остается несколько неизвестных. Если формула сложная, сначала подставьте в нее известные величины и решите уравнение относительно той переменной, значение которой нужно найти в задании. Если в задании две формулы, подумайте, как они связаны друг с другом.
Внимательно прочитайте условие и вопрос задачи, проверьте единицы измерения, если нужно — переведите одну в другую, особенно в физических задачах. Если получили два положительных ответа, проанализируйте, как правильно его указать в бланке: больший или меньший корень, их сумму или разность. Решив уравнение, перепроверьте ответ.

Одиннадцатое задание
Работа с графиком функции и ее свойствами.
Что знать. Вот какие темы стоит повторить:
- Алгоритм получения формулы, задающей функцию из графика этой функции.
- Общий вид формул, которыми задаются линейные, квадратичные, логарифмические, показательные, тригонометрические, а также формулы обратной пропорциональности и корня четной степени.
- Способы решения систем уравнений.
Совет. Решить задание быстрее помогут знания о сдвигах и форме графиков элементарных функций.

Двенадцатое задание
Работа с функциями — умение находить производные, наибольшее и наименьшее значение и так далее.
Что знать. Правила нахождения производной сложной функции и дифференцирования любых функций.
Совет. Не спешите находить производную — обратите внимание на свойства функции. Иногда для нахождения наибольшего или наименьшего значения функции можно воспользоваться возрастанием или убыванием.
Если видите, что надо найти наименьшее или наибольшее значение функции, ищите значение Y. А если в задании просят найти точку максимума или минимума — ищите значение Х.

Тринадцатое задание
Алгебраическое задание повышенного уровня сложности с развернутым ответом. В нем решают тригонометрические, показательные или логарифмические уравнения и отбирают корни, принадлежащие числовому промежутку.
Что знать. Способы и алгоритмы решения уравнений. Например, для решения показательных уравнений запомните свойства степеней.
Для решения тригонометрических — формулы приведения, формулы сложения и вычитания тригонометрических функций, основное тригонометрическое тождество, множество значений тригонометрических функций.
Обязательно нужно уметь отбирать корни уравнения на заданном промежутке с помощью тригонометрической окружности или на графике тригонометрической функции, или решая двойное неравенство.
Совет. При решении логарифмических уравнений помните про свойства логарифмов, про область определения и проверку.
Применяя свойства логарифмов в решении уравнений, можно расширить область определения или сузить ее. Если область определения расширилась, то лишние корни отметаются при проверке. А если область определения сузилась — в процессе решения корни могут потеряться.
В результате преобразований тригонометрические, логарифмические и показательные уравнения сводятся к совокупности простейших уравнений. Поэтому и добавили задание в перечень.
Знания, которые выпускник применяет в 13-м задании, пригодятся и для решения 15-го: по спецификации они проверяют одни и те же умения.

Четырнадцатое задание
Геометрическая задача с развернутым ответом — одно из самых сложных тематических заданий, поэтому его решение потребует времени. Вместе с тем до конца его решать тоже не обязательно.
Что знать. Пригодятся знания по разделам:
- Геометрические тела, их элементы и свойства.
- Признаки геометрических фигур.
- Способы доказательств.
Еще нужно уметь строить сечения и проводить доказательства, пользуясь изученными фактами.
Совет. В первой части задания важно соблюдать логику доказательства. Даже если не получилось доказать пункт А, его все равно можно использовать в пункте Б — как будто он уже верный.

Девятнадцатое задание
Большинство задач отсылают к целочисленной арифметике, то есть к математике 5—7 классов. У них исследовательский характер, поэтому нужно уметь подтвердить или опровергнуть выдвинутую гипотезу.
Что знать. Как можно больше о целых числах, их свойствах, уметь комбинировать известные способы и алгоритмы решения.
Совет. Первый пункт задачи доступен многим ученикам, так как не требует специальных знаний. Достаточно терпения и сообразительности, чтобы обнаружить подходящую математическую конструкцию.

Новости из мира образования, советы по карьере и учебе, вдохновляющие истории — в нашем телеграм-канале: @t_obrazovanie